Geometry module 1: congruence, proof, and constructions. module 1 embodies critical changes in geometry as outlined by the common core. the heart of the module is the study of transformations and the role transformations play in defining congruence. Dec polygon definition area of interior angles a 15, 2020 · the angles in a hexagon are 135^\circ, 62^\circ, 151^\circ, 140^\circ, x^\circ and\ (x +6)^\circ. find the measures of the missing angles. the area of a regular hexagon.
Interior Angle Formula Definition Examples Video
The sum of the interior angles of a triangle is always 180. so, if we know two angles, we can always find the third. an exterior angle is equal to the sum of the non-adjacent interior angles. Learn the interior angle formula for polygons, apply the formula to find the sum of the interior angles of a polygon, and use it to find an unknown interior angle. For example, a square has four interior angles all measuring 90 degrees. with sides drawn by straight lines (no curves) which together form a closed area. An angle inside a shape, between two joined sides.
An interior angle of a polygon is an angle formed inside the two adjacent sides of a polygon. or, we can say that the angle measures at the interior part of a polygon are called the interior angle of a polygon. we know that the polygon can be classified into two different types, namely: regular polygon; irregular polygon; for a regular polygon, all the interior angles are of the same measure. All interior angles in a regular polygon are equal (interior angles are congruent). once you know how to find the sum of interior angles, you can use that to find the measure of any interior angle, ∠a ∠ a, of a regular polygon. take the same formula and divide by the number of sides: ∠a = (n − 2) × 180° n ∠ a = (n 2) × 180 ° n.



Definition: the angles on the inside of a polygon formed by each pair of adjacent sides. try this adjust the polygon below by dragging any orange dot. click on " . In euclidean geometry, a regular polygon is a polygon that is equiangular (all angles are equal in measure) and polygon definition area of interior angles a equilateral (all sides have the same length). regular polygons may be either convex or star. in the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a straight line. Consecutive interior angles examples supplementary. these are three examples of consecutive angles that are also supplementary angles because they measure 180 degrees. complementary. there are also consecutive angles that are complementary because they measure 90 degrees. video: consecutive angles tutorial.
Geometry Module 1 Engageny
Once you know how to find the sum of interior angles of a polygon, finding one interior angle for any regular polygon is just a matter of dividing. where s s = the sum of the interior angles and n n = the number of congruent sides of a regular polygon, the formula is: s n s n here is an octagon (eight sides, eight interior angles). The polygon area is the region occupied by the polygon. the basic types of polygons are regular polygon and irregular polygon. learn about the area of a polygon, polygon definition, central point of a polygon, radius of the inscribed circle, circumscribed circle, and polygon of n sides. Irregular polygon. if all the sides and the interior angles of the polygon are of different measure, then it is known as an irregular polygon. for example, a scalene triangle, a rectangle, a kite, etc. convex polygon. if all the interior angles of a polygon are strictly less than 180 degrees, then it is known as a convex polygon.
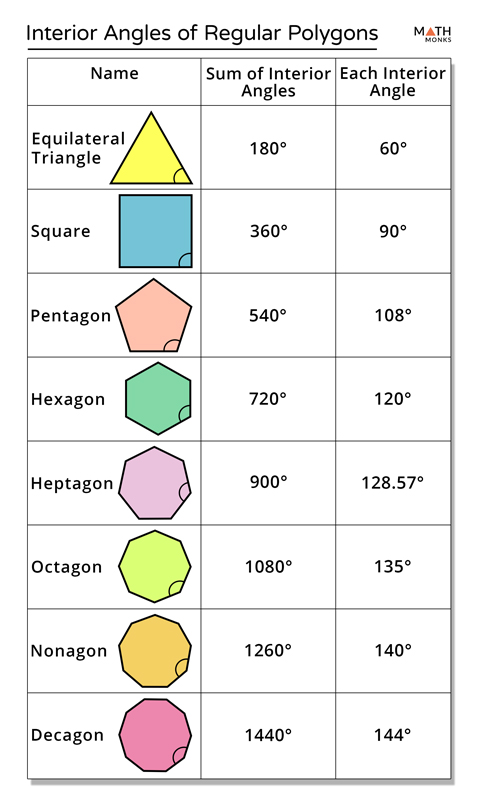
The sum of interior angles is \6 2) \times 180^\circ = 720^\circ\). one interior angle is \(720^\circ \div 6 = 120^\circ\).. exterior angles of polygons. if the side of a polygon is extended. Then i just have to multiply the number of triangles times 180 degrees to figure out what are the sum of the interior angles of that polygon as a function of the number of sides wikimatrix for a simple (non-self-intersecting) polygon regardless of whether it is convex or non-convex, this angle is called an interior angle (or internal angle ) if a point within the angle is in the interior of. The magnitude of an angle can be determined by the number of sides of the polygon. when the measure of one interior angle of a regular polygon is determined, it can be multiplied by the number of sides of the polygon to find the sum of the interior angles of the polygon. A convex polygon is defined as a polygon with all its interior angles less than 180°. this means that all the vertices of the polygon will point outwards, away from the interior of the shape. think of it as a 'bulging' polygon. note that a triangle (3-gon) is always convex. a convex polygon is the opposite of a concave polygon. see concave.
See more videos for interior angles area of a polygon definition. An interior angle is an angle inside a shape. example: another example: interior exterior angles. triangles. the interior angles of a triangle add up to 180 °.
The following diagram shows the formula for the sum of interior angles of an n-sided polygon and the size of an interior angle of a n-sided regular polygon. scroll down the page for more examples and solutions on the interior angles of a polygon. example: find the sum of the interior angles of a heptagon (7-sided) solution:. For a polygon: a line segment on the boundary joining one vertex (corner point) to another. example: this pentagon has 5 edges. for a polyhedron: a line segment where two faces meet. example: this polygon definition area of interior angles a tetrahedron has 6 edges:.
Interior angle (of a polygon) learnalberta. ca.
Polygons: formula and examples · interior angle sum theorem · definition of a regular polygon: · measure of a single interior angle · finding 1 interior angle of a . Solve the riddle: i am a polygon. i have two right angles. unit 15 section 2 : angle properties of polygons. polygons (geometry, points, lines, planes and angles. In geometry, a polygon is a plane figure that is described by a finite number of the area a of a simple polygon can also be computed if the lengths of the sides, a1, a2, an and the exterior angles, θ1, θ2, θn are . Only when vertical angles, a, are 45 ° can they be complementary. acute vertical angles could be complementary; you have a 1-in-45 chance of that. complementary angles example complementary angles add to 90 °. complementary angles need not be connected with a common vertex or point, or line. they can be adjacent or vertical in intersecting lines.
Interior angles of a polygon formula. the interior angles of a polygon always lie inside the polygon. the formula can be obtained in three ways. let us discuss the three different formulas in detail. method 1: if “n” is the number of sides of a polygon, then the formula is given below: interior angles of a regular polygon = [180°(n. The interior angles of a polygon are those angles at each vertex that are on the inside of the polygon. there is one per vertex. so for a polygon with n sides, there are n vertices and n interior angles. for a regular polygon, by definition, all the interior angles are the same. in the figure above, click on "make regular" then change the. A convex polygon is a simple polygon (not self-intersecting) in which no line segment between two points on the boundary ever goes outside the polygon. equivalently, it is a simple polygon whose interior is a convex set. in a convex polygon, all interior angles are less than or equal to 180 degrees, while in a strictly convex polygon all interior angles are strictly less than 180 degrees. We can use a formula to find the sum of the interior angles of any polygon. in this polygon definitions, p olygon formulas (area, perimeter) and polygon names .
0 Response to "Polygon Definition Area Of Interior Angles A"
Post a Comment